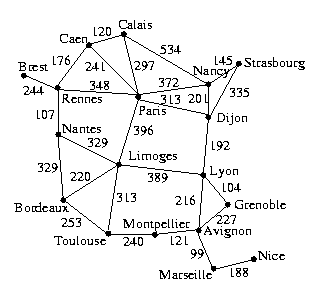
Use the following latitudes and longitudes for the cities to write a function that returns the estimated distance between two cities.
Paris, 48:51:00N 2:20:00E Caen, 49:15:00N 0:20:00W Calais, 50:57:36N 1:57:00E Dijon, 47:21:00N 5:02:00E Lyon, 45:44:00N 4:52:00E Grenoble, 45:21:36N 5:19:12E Avignon, 43:50:00N 4:45:00E Marseille, 43:18:00N 5:25:00E Nice, 43:42:00N 7:21:00E Montpellier, 43:38:00N 3:53:00E Toulouse, 43:37:00N 1:27:00E Bordeaux, 44:50:00N 0:37:00W Limoges, 45:30:00N 1:10:00E Rennes, 48:07:00N 1:02:00W Brest, 48:24:00N 4:30:00W Strasbourg, 48:32:24N 7:37:34E Nancy, 48:50:00N 6:10:00E Nantes, 47:15:00N 1:30:00W
The file graph.txt should help you save a few keystrokes, especially if you know how to program. There is also a copy of this file on cs-class, which you can copy by executing
cs-class% cp ~maloofm/cosc270/graph.txt ./Note that each entry in the property list for a city should consist of three items: the state, the action that leads to the state, and the action cost. For example, for Nice, its property list should be:
(setf (get 'nice 'adj) '((marseille va-marseille 188)))
- successors problem state ⇒ ((successor action action-cost)* ),
- make-child node successor ⇒ (state path path-cost),
- goal-test problem state ⇒ [ t | nil ],
- h node goal ⇒ Number, and
- f node goal ⇒ Number.
Recall that g node ≡ path-cost. Put the weighted graph and these problem-specific functions in a file named france.lisp.
- uniform-cost search as the function ucs,
- greedy best-first search as the function gbfs, and
- A* as the function a*.
As we discussed in lecture, each search function should take a problem as its only argument and return a pair consisting of the solution (i.e., a sequence of actions) and the solution's cost. Put these functions in a file named main.lisp
For the problem passed to these functions, the implementations should assume that the parameter problem will have the properties start-state and goal-state to store the initial and goal states for a problem, respectively. For example,
(setf (get 'problem 'start-state) 'nice) (setf (get 'problem 'goal-state) 'marseille)Then,
> (ucs 'problem) ((VA-NARSEILLE) 188.0)
It is imperative that you name and implement these functions correctly. To grade your project, I will use my own functions to automatically call and evaluate your implementations. I will also evaluate your implementations using different search problems.
Clearly, if you haven't named or implemented these functions correctly, then my routines won't work with your code. You should think about other types of problems I might use and the special cases your search routines might need to handle. As a simple example, how do your implementations handle the case that the goal state of a graph is not reachable from the initial state?
All variables must be either a function parameter or locally scoped in let or do forms. Your implementations must not rely on global variables and must not litter memory with global variables as they execute.
- the average number of nodes explored or entered
- the average number of nodes expanded (i.e., the total number of successors)
- the average number of nodes maintained (i.e., stored in the frontier)
- the average number of times it found the optimal solution
| Run | Initial State | Goal State |
| 1 | Brest | Marseille |
| 2 | Montpellier | Calais |
| 3 | Strasbourg | Bordeaux |
| 4 | Paris | Grenoble |
| 5 | Grenoble | Paris |
| 6 | Brest | Grenoble |
| 7 | Grenoble | Brest |
Place the solutions, path costs, and the statistics in a file named README. Write a paragraph that compares and contrasts the search algorithms in terms of these statistics. What differences or similarities do you see between the informed search algorithm and the optimal search algorithms? What differences or similarities do you see between the two optimal search algorithms. Include this file with your submission.
Instructions for Electronic Submission
The name of the file containing your Lisp functions must be named main.lisp. In a file named HONOR, provide the following information:Name NetID In accordance with the class policies and Georgetown's Honor Code, I certify that, with the exceptions of the course materials and those items noted below, I have neither given nor received any assistance on this project.
When you are ready to submit your project, create the zip file for uploading by typing:
$ zip submit.zip main.lisp france.lisp README HONORUpload submit.zip to Autolab. You can submit to the compile check p1c seven times. You can submit your assignment p2 twice, but you won't see the output from the autograder until I review, grade, and return your project.
Plan B
If Autolab is down, upload your zip file to Canvas.
Copyright © 2019 Mark Maloof. All Rights Reserved. This material may not be published, broadcast, rewritten, or redistributed.