COSC 160: Data Structures

Project 5
Fall 2021

Due: M 12/6 @ 11:59 PM
9 points

Last one! Woo hoo! \o/ In this project, you are going to implement a data structure and algorithms for graphs using either an adjacency list or an adjacency matrix.

Naturally, I put some starter code on cs-class-1, which you can retrieve using the command: 

cs-class-1% cp ~maloofm/cosc160/p5.zip ./

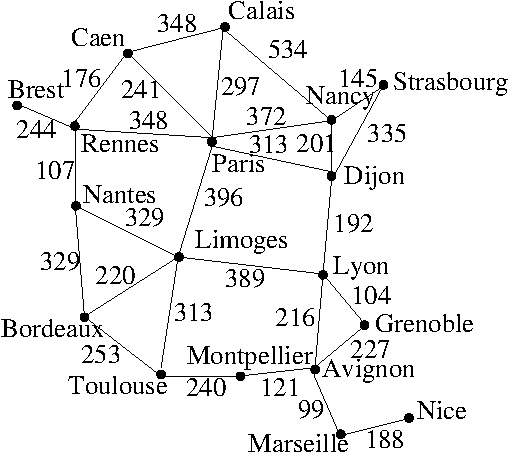
In addition to the class definitions, the file france-graph.dta is an example of the file format for graphs. The information in this file represents a road network in France:

The first line of the file contains a single character that indicates the type of graph with U indicating an undirected graph and D indicating a directed graph. (I use this value to format edge names.) The second line contains a single integer that indicates the number of vertices in the graph. The second line consists of the vertex names. The remaining lines contain the connectivity information for the vertices in the order they appear on the second line in the form of a matrix, which you can process and store in an adjacency list or adjacency matrix.

Undirected graphs have matrices that are symmetric with entries that are either zero (unconnected) or greater than zero (connected). Directed graphs have matrices that may not be symmetric with entries that are either zero (unconnected) or greater than zero (connected). Unweighted graphs will have non-zero entries equal to one. Weighted graphs will have non-zero entries greater than or equal to one. There is no reason for us to distinguish between weighted and unweighted graphs.

The method Graph::read reads a file in this format and constructs the graph accordingly. When reading graph information, you do not need to worry about error handling or improperly formatted input files. Naturally, you will want to construct your own graphs to test aspects of your implementation.

As for the algorithms you will implement,

  1. implement Graph::dfsTraversal (Code Fragment 13.17).
  2. implement Graph::components, which computes the components of the Graph. Its implementation is similar to Code Fragment 13.9.
  3. implement PathFinder, which uses Graph::dfsTraversal via inheritance and polymorphism and Path to find paths between two vertices. Its implementation is similar to Code Fragment 13.13, 13.14, and 13.15.
  4. implement Djikstra's algorithm (Code Fragment 13.24) as Graph::shortestPath. For the priority queue, implement a min-heap with location-aware entries as the class Heap<K,T>.

As you can see from the class definitions, you will need to implement additional methods.

Instructions for Electronic Submission: In a file named HONOR, please include the statement: 

In accordance with the class policies and Georgetown's Honor Code,
I certify that, with the exceptions of the class resources and those
items noted below, I have neither given nor received any assistance
on this project.
Include this file in your zip file submit.zip.

Submit p5 exactly like you submitted p4. Make sure you remove all debugging output before submitting.

Plan B

If something goes wrong with Autolab, upload your zip file to Canvas.

Copyright © 2020 Mark Maloof. All Rights Reserved. This material may not be published, broadcast, rewritten, or redistributed.